Температурные воздействия на конструкции – Часть 2: Термомеханика

В этой части рассмотрены теоретические основы температурных воздействий на конструкции с точки зрения классической механики материалов.

В предыдущей части 1 рассмотрены особенности учета температурных воздействий при проектировании конструкций зданий по российскому своду правил СП 20.13330.2011 (СНиП 2.01.07-85).

В части 3 представлены примеры температурных воздействий на простые конструкции – балки с различными условиями закрепления.

Теоретические основы температурных воздействий на материалы

Температурное расширение-сокращение

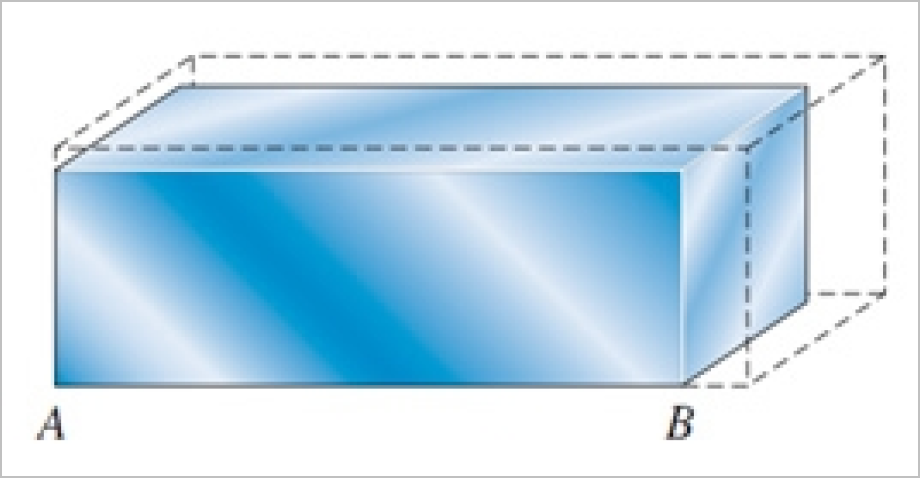Изменения температуры вызывают расширение или сокращение конструкционных материалов, в результате чего в них возникают температурные деформации и температурные напряжения. Простая иллюстрация температурного расширения, где брусок материала не закреплен и поэтому имеет возможность свободно расширяться [1].

Когда этот брусок нагревается, каждый элемент материала подвергается температурным деформациям по всем направлениям, и, соответственно, размеры бруска увеличиваются также во всех направлениях. Если взять угол А за точку отсчета и дать стороне АВ возможность сохранять свое исходное направление, то брусок примет форму, которая показана штриховыми линиями.

Для большинства конструкционных материалов температурная деформация εT является пропорциональной изменению температуры ΔT, то есть

εT = α·ΔT, (1)

где α – свойство материала, которое называется коэффициентом температурного расширения. Согласно принятому в мире «знаковому соглашению» температурное расширение считается положительным, а температурное сокращение – отрицательным [1, 2].

Коэффициент температурного расширения конструкционных материалов

Поскольку деформация является безразмерной величиной, этот коэффициент температурного расширения имеет размерность, обратную изменению температуры. В системе СИ размерность αТ может выражаться как 1/К (величина обратная единице СИ Кельвин) или 1/ºС (величина обратная градусу Цельсия). Величина αТ является одинаковой в обоих случаях, так как изменение температуры является численно одинаковым как в градусах Кельвина, так и в градусах Цельсия.

Удобно представлять величину коэффициента температурного расширения в единицах 10-6/ºС или мкм/м·ºС. Последний вид особенно удобен – он наглядно показывает насколько микрометров удлиняется один метр материала при увеличении температуры на один градус температуры.

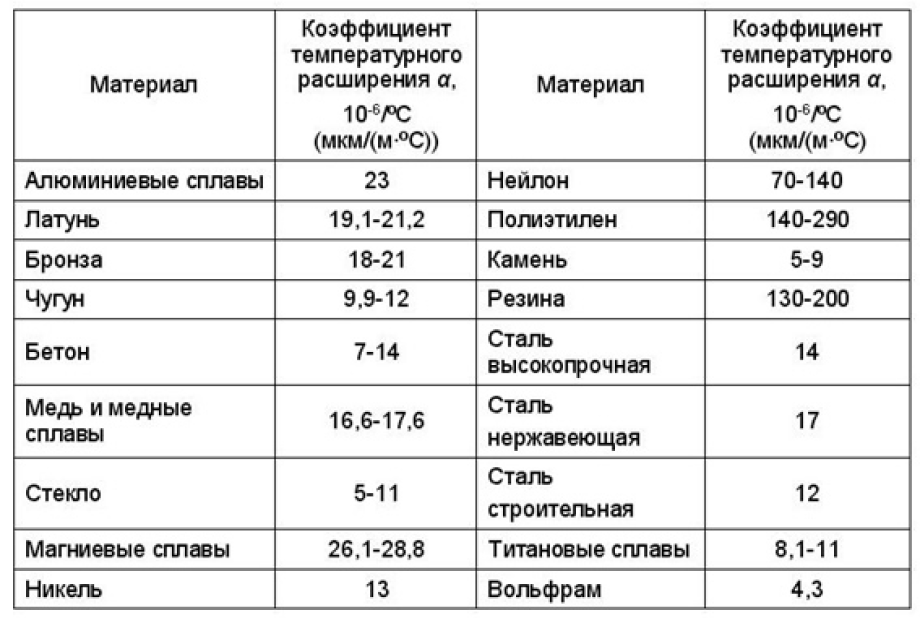
Информация о коэффициентах температурного расширения некоторых конструкционных материалов представлена в таблице.

Коэффициент температурного расширения алюминиевых сплавов

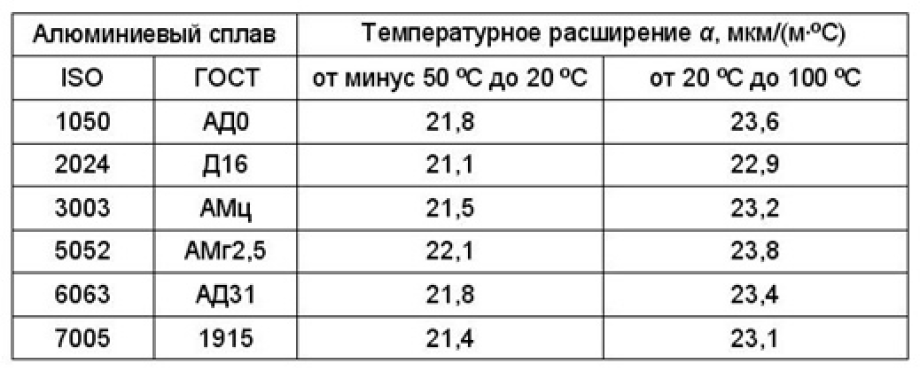Коэффициенты температурного расширения основных алюминиевых сплавов, которые применяются в строительстве, показаны в таблице.

Из таблицы видно, что коэффициенты температурного расширения различных алюминиевых сплавов различаются незначительно. Поэтому в своде правил СП 128.13330.2012 (СНИП 2.03.06-85) для расчетов алюминиевых конструкций в интервале температуры от минус 70 ºС до 100 ºС для всех применяемых в строительстве алюминиевых сплавов применяется коэффициент температурного расширения 0,23·10-4 1/ºС [4]. В европейском стандарте EN 1991-1-5 величина расчетного коэффициента температурного расширения составляет 24·10-6 1/ºС [5].

Температурные напряжения

Чтобы продемонстрировать относительную важность температурных напряжений, можно сравнить температурные напряжения с напряжениями, которые возникают при силовом нагружении [1]. Предположим, что мы имеем брус, который нагружен силами в осевом направлении с продольными деформациями, которые даются равенством

ε = σ/Е, (2)

где σ – напряжение, а Е – модуль упругости. Далее предположим, что мы имеем идентичный брусок, которые подвержен изменению температуры ΔT. Это означает, что этот брусок имеет температурные деформации согласно равенства (1). Приравнивание этих двух видов деформаций дает уравнение

σ = Е·α·ΔT (3)

Пример

Вычислим осевое напряжение σ, которое дает такие же деформации, как и изменение температуры ΔT в стержнях из алюминиевого сплава и строительной (малоуглеродистой) стали при увеличении их температуры на 50 ºС.

Для алюминиевого стержня (α = 23·106, Е = 70000 Н/мм2):

σ = 70000·23·10-6·50 = 80,5 Н/мм2

Для стержня из малоуглеродистой стали (α = 12·106, Е = 210000 Н/мм2):

σ = 210000·12·10-6·50 = 126 Н/мм2

Отметим известный факт, что при одинаковом изменении температуры температурные напряжения в алюминиевом стержне составляют только 2/3 от величины температурных напряжений в стальном стержне. Так происходит потому, что величина температурных напряжений зависит от произведения модуля упругости и коэффициента температурного расширения (см. формулу (3)). Поэтому, хотя коэффициент температурного расширения алюминия в два раза больше, чем у стали, но модуль упругости алюминия в три раза меньше, чем у стали.

Как видно из приведенных выше расчетов, температурные напряжения могут достигать величин, сравнимых с напряжениями от механических нагрузок. Поэтому термические воздействия на конструкции зданий необходимо учитывать наряду с другими нагрузками, как того и требуют нормативные документы [4, 5].

Температурные перемещения

Вернемся к бруску материала, показанного на рисунке 1 [1]. Предполагаем, что материал бруска является гомогенным и изотропным, то есть механические свойства материала бруска являются одинаковыми во всем его объеме. Кроме того, предполагаем, что изменение температуры ΔT является однородным, то есть одинаковым, по всему бруску. При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину

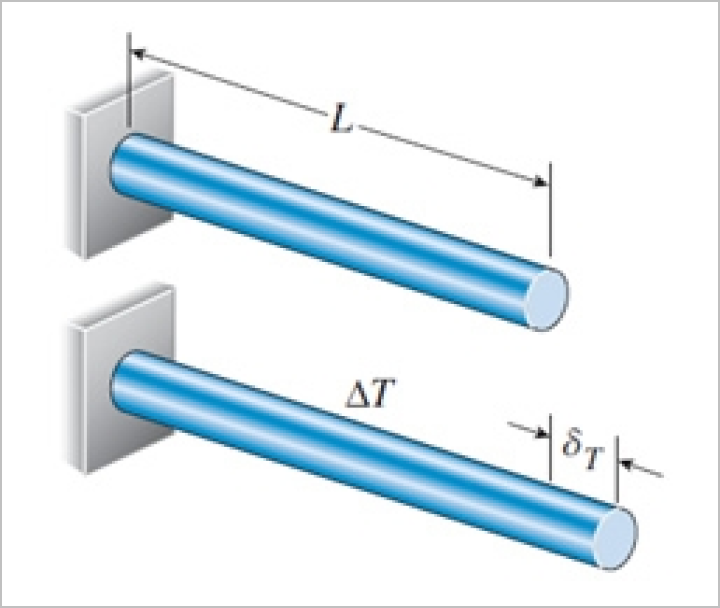
δТ = εT· L= α·ΔT·L (4)

Уравнение (4) можно применять для вычисления изменений длин элементов конструкций после однородного нагрева, например, удлинение призматического стержня на рисунке 2.2. Поперечные размеры стержня также изменятся, но эти изменения не показаны на рисунке 2.2, так как обычно они не оказывают влияния на осевые силы, которые передаются этим стержнем.

Пример

Оценим удлинение незакрепленных алюминиевого и стального стержней длиной 3 м при увеличении их температуры на 50 ºС.

Для алюминиевого стержня:

δТ = α·ΔT·L = 23·10-6·50·3000 = 3,5 мм

Для стержня из малоуглеродистой стали:

δТ = α·ΔT·L = 12·10-6·50·3000 = 1,8 мм

При рассмотрении выше температурных деформаций предполагалось, что конструкция не имеет ограничений для своих перемещений, что позволяло ей расширяться или сокращаться совершенно свободно. Такие условия возникают, например, когда объект лежит на гладкой поверхности, на которой не возникает трения [1]. В таких случаях при однородном нагреве всего объекта в целом не возникает напряжений, хотя неоднородные изменения температуры могут вызывать внутренние температурные напряжения. Однако многие конструкции имеют опоры, которые препятствуют свободному расширению и сокращению их размеров. Поэтому в них развиваются температурные напряжения даже, если изменение температуры является однородным по всей конструкции.

Температурные деформации в статически определимых конструкциях

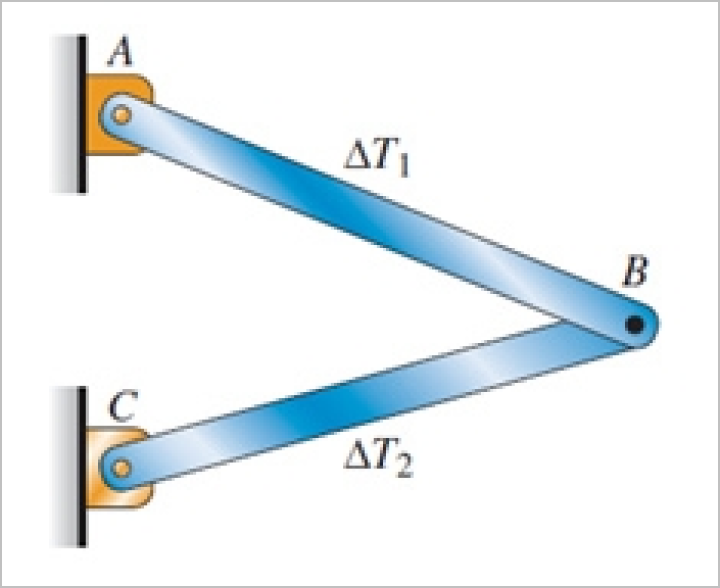
Рассмотрим ферму АВС из двух стержней, показанную на рисунке 2.3. Предположим, что температура стержня АВ изменилась на ΔТ1, а стержня ВС – на ΔТ2. Поскольку эта ферма является статически определимой, то оба стержня могут свободно удлиняться или укорачиваться, давая в результате перемещение соединения В. Однако в этом случае температурные напряжения в стержнях, а также реакции в опорах, отсутствуют.

Это заключение справедливо в целом для всех статически определимых конструкций, а именно: однородное изменение температуры в элементах конструкции вызывают температурные деформации (и соответствующие изменения длин элементов) без возникновения соответствующих температурных напряжений [1, 2].

Температурные деформации в статически неопределимых конструкциях

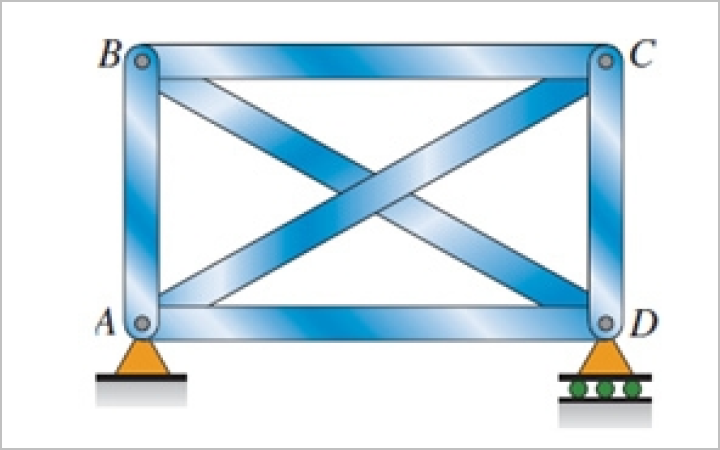
Статически неопределимыми конструкциями называются конструкции, у которых число реакций превышает число уравнений статического равновесия. В отличие от статически определимых конструкций при расчете таких конструкций принимаются во внимание прогибы [1, 2].

В статически неопределимой конструкции температурные напряжения могут возникать или не возникать в зависимости от особенностей конструкции и особенностей температурных изменений. Чтобы проиллюстрировать некоторые из таких возможностей, рассмотрим статически неопределимую ферму.

Опоры этой конструкции позволяют узлу D двигаться горизонтально. Поэтому, когда вся ферма однородно нагревается, в ней не возникает температурных напряжений. Все элементы увеличиваются в длине пропорционально своим первоначальным длинам, а вся ферма в целом становится немного больше в размерах.

Однако, если некоторые из стержней нагреваются, а другие – нет, то возникают температурные напряжения, так как статически неопределимое расположение стержней препятствует их свободному расширению.

заключение

1. Изменение температуры элементов конструкции вызывает в них температурные деформации. Температурные напряжения возникают только в статически неопределимых конструкциях.
2. Однородный нагрев алюминиевого стержня на 50 ºС способен при жестком закреплении концов стержня вызывать значительные температурные напряжения. При таком нагреве удлинение стержня со свободными концами составляет 3,5 мм.