Температурные нагрузки на конструкции - Часть 3: Примеры

В этой, заключительной, части представлены примеры температурных воздействий на простейшие теоретические конструкции – балки с различными условиями закрепления.

В части 1 были рассмотрены особенности учета температурных воздействий при проектировании конструкций зданий по СП 20.13330.2011 (СНиП 2.01.07-85).

В части 2 были рассмотрены теоретические основы температурных воздействий на конструкции с точки зрения классической механики материалов.

Основные термомеханические соотношения

Фундаментальным соотношением, которое описывает поведение конструкций под воздействием термических воздействий, является следующее [1, 2]:

εtot = εT + εm

Деформированное состояние конструкции задает полная деформация εtot за счет кинематических соотношений или условий совместности. Напряженное состояние конструкции – упругое или пластическое – зависит только от механической составляющей деформаций εm.

Деформации температурного расширения имеют следующий вид:

εT = αΔT

где α — коэффициент температурного расширения.

Подробнее о механике температурных деформаций и напряжений см. часть 2.

Параметры температурного воздействия на конструкционные элементы

Согласно СНиП 2.01.07-85 основными параметрами термического воздействия на конструкционные элементы являются (см. часть 1):

• однородное изменение температуры элемента и
• перепад температуры (градиент температуры) по толщине элемента.

В реальных конструкциях под воздействием температурных воздействий возникают сложные комбинации температурных деформаций и напряжений. Ниже на примере балок с различными закреплениями концов представлены основные закономерности поведения элементов конструкций при их однородном нагреве и нагреве с перепадом (градиентом) по толщине.

Для определенности будем ниже предполагать, что рассматриваемые конструкционные элементы – балки – подвергаются нагреву, а не охлаждению. Обычно основные проблемы термического воздействия связаны именно с чрезмерным нагревом элементов конструкций.

Однородный нагрев балок

Свободно опертая балка

В этом случае результатом нагрева будет простое удлинение балки на величину lαΔT. При этом полная деформация εtot равна температурной деформации εT, а механические деформации εm отсутствуют. Это означает, что в балке не возникает температурных напряжений.

Двухшарнирная балка

Другим идеальным случаем является балка с шарнирными неподвижными опорами при небольшом однородном нагреве ΔT. В этом случае полная деформация εtot равна нулю, так как перемещения концов балки отсутствуют. Температурное расширение компенсируется равным по величине и противоположным по знаку сжимающими силами Р, которые возникает в опорах.

В результате в балке возникает напряжение σ величиной Eεm. Величина силы реакции опор Р составляет

P = EAεm = –EAεT = –EAα∆T,

где А – площадь сечения балки.

При дальнейшем увеличении однородного нагрева балки (увеличения ΔT) может возникать два основных варианта поведения балки в зависимости от степени ее гибкости [3].

Короткая (негибкая) двухшарнирная балка

Если балка достаточно короткая (или толстая), то с продолжением нагрева под действием температурных напряжений ее материал достигает предела текучести, после чего будет происходить однородное пластическое деформирование балки без прогиба.

Нагрев ΔTy, при котором происходит достижение предела текучести материала σy, определяется по формуле:

ΔTy = σy/EA

Длинная (гибкая) двухшарнирная балка

Если балка имеет достаточно высокую гибкость, то происходит ее упругое выпучивание еще до достижения предела текучести материала. Критическая нагрузка Pcr (нагрузка Эйлера) для балки вычисляется по формуле

Pcr = (π2EI)/l2.

Приравнивая это выражение к выражению для силы реакции Р, получаем

E*A*α*ΔT = (π2EI)/l2,

что приводит к выражению для определения критической температуры выпучивания балки

ΔTcr = (π2/α)(r/l)2

или

ΔTcr = π2/(α λ2)

Здесь: r – так называемый радиус гиратации и λ – коэффициент гибкости (l/r) [1, 2].

Если температура будет и дальше повышаться, то балка будет продолжать выпучиваться[3].

Выше приведенные случаи представляют два фундаментальных вида реакции балок, которые подвержены температурному расширению при ограничении перемещения их концов: пластическое деформирование или выпучивание. Кроме того, может возникать более сложная реакция балки, которая состоит из комбинации пластического деформирования и выпучивания [3].

Выпучивание двухшарнирной балки под воздействием однородного нагрева [2]

Балка с частичным ограничением осевого перемещения

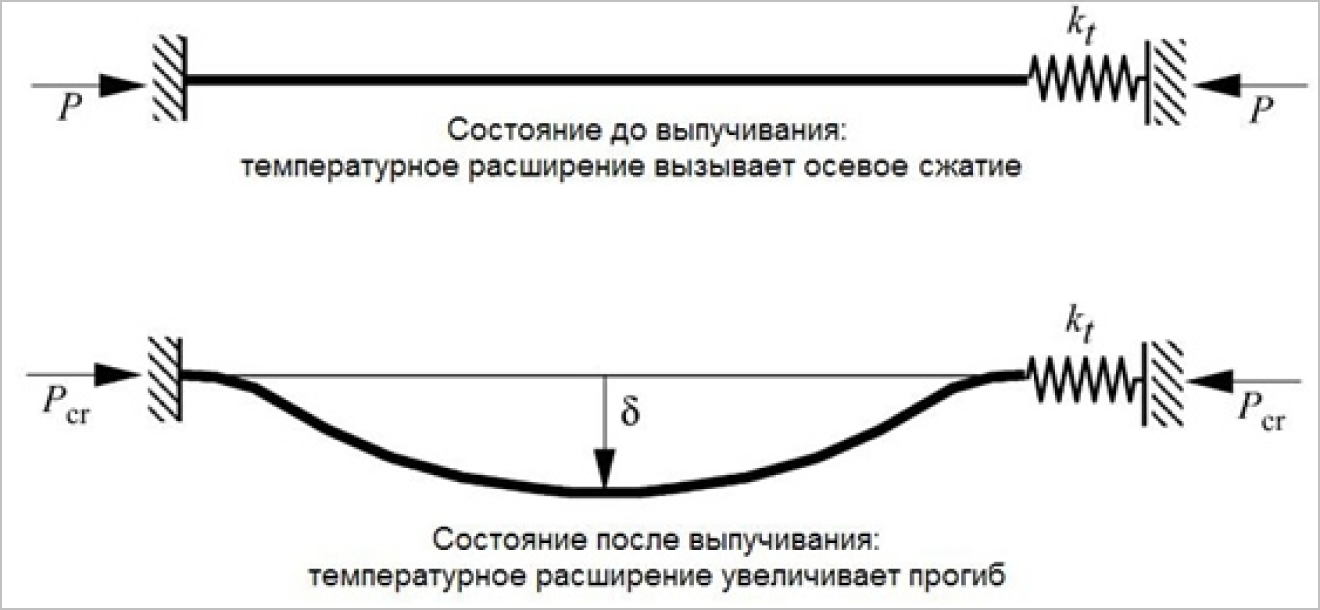
Нагрев балки с частичным ограничением осевого перемещения [2]

Выше предполагалось, что осевое перемещение концов балки абсолютно жестко ограничено. Этот случай является верхним пределом и практически недостижимым в реальных конструкциях, так как они всегда могут обеспечивать только частичное ограничение осевого перемещения концов балки.

На рисунке 3.4 показана такая балка, у которой осевое перемещение ограничено только частично с помощью пружины с жесткостью kt. В этом случае под действием температурного расширения будет развиваться сжимающее осевое напряжение

P = –E*α*∆T /(1 + EA/ktL)

Критическое повышение температуры балки будет задаваться выражением

ΔTcr = π2 (1 + EA/ktL) /(α λ2) (*)

Зависимость критического нагрева ΔTcr, при котором происходит выпучивание балки, от жесткости ограничения ее осевого перемещения [2]

Графики получены по формуле (*) [2]. Они показывают зависимость температуры выпучивания от гибкости балки при различной жесткости пружины kt. Чем больше жесткость пружины, тем при меньшей гибкости балки происходит ее выпучивание.
При нагреве до 100 ºС при абсолютно жесткой заделке выпучивание балки происходит уже при гибкости λ, равной около 90, а при минимальной жесткости пружины (λ = EA/l), то есть более свободном закреплении – только при гибкости λ, более 135.

нагрев балки с перепадом по толщине (градиентный нагрев)

При нагреве конструкции под воздействием, например, солнечного излучения, температура наружной поверхности балки будет выше, чем ее внутренняя поверхность. При этом температурное расширение наружной поверхности будет больше, чем внутренней поверхности, что вызывает прогиб балки. Это явление называется термическим прогибом.

Свободно опертая балка

На рисунке 3.6 схематически показан изгиб свободно опертой балки под воздействием однородного температурного градиентом по толщине балки d (в направлении оси y):

gradyT = (T2 – T1)/d

Двухшарнирная балка

Балка с двумя неподвижными шарнирными опорами под воздействием температурного градиента [2]

Если температурный градиент прилагается к двухшарнирной балке с закрепленными опорами, то результатом его воздействия будут прогиб балки и соответствующие реакции в опорах.

Балка с двумя заделанными концами

Балка с заделанными концами под воздействием однородного градиента температуры [2]

На рисунке показана балка с заделанными концами (путем добавления ограничения поворотов концов балки на рисунке 3-7) под воздействием однородного градиента температуры по ее толщине.

Такой градиент температуры вызывал бы прогиб балки со свободно опертыми концами, который показан на рисунке 3-6. Однако в местах заделки концов балки возникают реакции в виде моментов М, которые обеспечивают то, что ось балки остается прямолинейной. Выражение для вычисления этого момента имеет вид

M = E*I*α*gradyT

Балка с частично заделанными концами

Абсолютно жесткую заделку также не просто выполнить в реальных конструкциях, как и абсолютно неподвижные шарниры. На рисунке показана балка с частично заделанными концами. Частичную заделку моделируют спиральные пружины с конечной жесткостью kr.

под воздействием однородного градиента температуры [2]

В этом случае момент реакции на спиральных пружинах при градиентном нагреве балки будет иметь вид
M = E*I*α*gradyT/(1 + 2EI/krl)

Это выражение показывает, балка с частичной заделкой концов под воздействием градиента температуры имеет меньший прогиб, чем при абсолютно жесткой заделке.

Заключение

Представлены примеры поведения простейших строительных конструкций – балок – с различными видами закрепления концов под температурными воздействиями. Показано, что вид условия закрепления концов балок оказывают большое влияние на величину возникающих температурных напряжений и прогибов. На условия закрепления балок влияет тип крепления (жесткая заделка, шарнир, свободное опирание), вид крепежа (болтовое, винтовое, заклепочное), количество крепежных элементов, расстояние между ними, форма отверстий под крепеж и т. д.